Contoh Soal Determinan Matriks Ordo 2×2 dan 3×3 beserta Jawabannya

Matriks adalah salah satu materi dalam pelajaran Matematika. Yuk, belajar mengerjakan contoh soal matriks bersama Mamikos!

24 Februari 2025 Lintang Filia

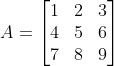14. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ , berapakah invers dari matriks $A$ ?

a. Matriks A tidak memiliki invers.

b. $\begin{bmatrix} -1 & 0 & 1 \\ 2 & -1 & 0 \\ -1 & 2 & -1 \end{bmatrix}$

c. $\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}$

d. $\begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

Jawaban: a. Matriks A tidak memiliki invers.

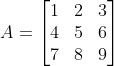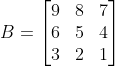15. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ dan $B = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix}$ , berapakah hasil perkalian 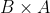$B \times A$ ?

a. $\begin{bmatrix} 90 & 114 & 138 \\ 54 & 69 & 84 \\ 18 & 24 & 30 \end{bmatrix}$

b. $\begin{bmatrix} 90 & 69 & 48 \\ 114 & 87 & 60 \\ 138 & 105 & 72 \end{bmatrix}$

c. $\begin{bmatrix} 90 & 114 & 138 \\ 69 & 87 & 105 \\ 48 & 60 & 72 \end{bmatrix}$

d. $\begin{bmatrix} 90 & 114 & 138 \\ 114 & 87 & 60 \\ 138 & 105 & 72 \end{bmatrix}$

Jawaban: d. $\begin{bmatrix} 90 & 114 & 138 \\ 114 & 87 & 60 \\ 138 & 105 & 72 \end{bmatrix}$

Contoh Soal Determinan Matriks Ordo 2×2 dan 3×3 – 4

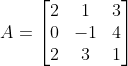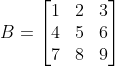16. Berapakah hasil dari $\text{Tr}(A^T B)$ jika $A = \begin{bmatrix} 2 & 1 & 3 \\ 0 & -1 & 4 \\ 2 & 3 & 1 \end{bmatrix}$ dan $B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ ?

a. 64

b. 94

c. 84

d. 74

Jawaban: d. 74

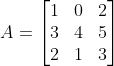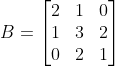17. Apabila $A = \begin{bmatrix} 1 & 0 & 2 \\ 3 & 4 & 5 \\ 2 & 1 & 3 \end{bmatrix}$ dan $B = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 3 & 2 \\ 0 & 2 & 1 \end{bmatrix}$ , berapakah hasil penjumlahan 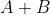$A + B$ ?

a. $\begin{bmatrix} 3 & 1 & 2 \\ 4 & 7 & 7 \\ 2 & 3 & 4 \end{bmatrix}$

b. $\begin{bmatrix} 4 & 1 & 2 \\ 4 & 7 & 7 \\ 2 & 3 & 4 \end{bmatrix}$

c. $\begin{bmatrix} 3 & 1 & 2 \\ 4 & 6 & 7 \\ 2 & 3 & 4 \end{bmatrix}$

d. $\begin{bmatrix} 4 & 1 & 2 \\ 3 & 7 & 7 \\ 2 & 3 & 4 \end{bmatrix}$

Jawaban: a. $\begin{bmatrix} 3 & 1 & 2 \\ 4 & 7 & 7 \\ 2 & 3 & 4 \end{bmatrix}$

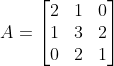18. Jika $A = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 3 & 2 \\ 0 & 2 & 1 \end{bmatrix}$ , berapakah invers dari matriks $A$ ?

a. $\begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix}$

b. $\begin{bmatrix} 2 & 1 & 0 \\ 1 & 3 & 2 \\ 0 & 2 & 1 \end{bmatrix}$

c. $\begin{bmatrix} 1 & 0 & 2 \\ 3 & 4 & 5 \\ 2 & 1 & 3 \end{bmatrix}$

d. Matriks A tidak memiliki invers.

Jawaban: a. $\begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix}$

19. Berapakah determinan dari matriks 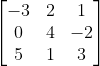$\begin{bmatrix} -3 & 2 & 1 \\ 0 & 4 & -2 \\ 5 & 1 & 3 \end{bmatrix}$ ?

a. -1

b. 1

c. -7

d. 7

Jawaban: c. -7

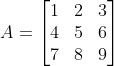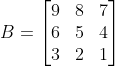20. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ dan $B = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix}$ , berapakah hasil dari $\text{Tr}(AB^T)$ ?

a. 54

b. 69

c. 99

d. 84

Jawaban: d. 84

Penutup

Demikian kumpulan contoh soal determinan matriks ordo 2×2 dan 3×3 dari Mamikos khusus untuk kamu belajar.

Apabila kamu masih ingin mengerjakan contoh soal Matematika lain, jangan lupa untuk membuka blog Mamikos, ya!

Referensi:

Rumus Determinan Matriks: Jenis, Sifat, Contoh Soal, dan Cara Menghitungnya [Daring]. Tautan: https://www.detik.com/edu/detikpedia/d-6937943/rumus-determinan-matriks-jenis-sifat-contoh-soal-dan-cara-menghitungnya

Rumus dan Contoh Determinan Matriks [Daring]. Tautan: https://www.gramedia.com/literasi/rumus-dan-contoh-determinan-matriks/

Halaman:

Klik dan dapatkan info kost di dekat kampus idamanmu:

Kost Dekat UGM Jogja

Kost Dekat UNPAD Jatinangor

Kost Dekat UNDIP Semarang

Kost Dekat UI Depok

Kost Dekat UB Malang

Kost Dekat Unnes Semarang

Kost Dekat UMY Jogja

Kost Dekat UNY Jogja

Kost Dekat UNS Solo

Kost Dekat ITB Bandung

Kost Dekat UMS Solo

Kost Dekat ITS Surabaya

Kost Dekat Unesa Surabaya

Kost Dekat UNAIR Surabaya

Kost Dekat UIN Jakarta

Contoh Soal Determinan Matriks Ordo 2×2 dan 3×3 beserta Jawabannya

14. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ , berapakah invers dari matriks $A$ ?

15. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ dan $B = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix}$ , berapakah hasil perkalian $B \times A$ ?

Contoh Soal Determinan Matriks Ordo 2×2 dan 3×3 – 4

16. Berapakah hasil dari $\text{Tr}(A^T B)$ jika $A = \begin{bmatrix} 2 & 1 & 3 \\ 0 & -1 & 4 \\ 2 & 3 & 1 \end{bmatrix}$ dan $B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ ?

17. Apabila $A = \begin{bmatrix} 1 & 0 & 2 \\ 3 & 4 & 5 \\ 2 & 1 & 3 \end{bmatrix}$ dan $B = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 3 & 2 \\ 0 & 2 & 1 \end{bmatrix}$ , berapakah hasil penjumlahan $A + B$ ?

18. Jika $A = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 3 & 2 \\ 0 & 2 & 1 \end{bmatrix}$ , berapakah invers dari matriks $A$ ?

19. Berapakah determinan dari matriks $\begin{bmatrix} -3 & 2 & 1 \\ 0 & 4 & -2 \\ 5 & 1 & 3 \end{bmatrix}$ ?

20. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ dan $B = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix}$ , berapakah hasil dari $\text{Tr}(AB^T)$ ?

Penutup

Tentang Kami

Job Mamikos

Promosikan Kost Anda

Pusat Bantuan

Blog Mamikos

Singgahsini

14. Jika , berapakah invers dari matriks ?

15. Jika dan , berapakah hasil perkalian ?

Contoh Soal Determinan Matriks Ordo 2×2 dan 3×3 – 4

16. Berapakah hasil dari jika dan ?

17. Apabila dan , berapakah hasil penjumlahan ?

18. Jika , berapakah invers dari matriks ?

19. Berapakah determinan dari matriks ?

20. Jika dan , berapakah hasil dari ?

Penutup

14. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ , berapakah invers dari matriks $A$ ?

15. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ dan $B = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix}$ , berapakah hasil perkalian $B \times A$ ?

16. Berapakah hasil dari $\text{Tr}(A^T B)$ jika $A = \begin{bmatrix} 2 & 1 & 3 \\ 0 & -1 & 4 \\ 2 & 3 & 1 \end{bmatrix}$ dan $B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ ?

17. Apabila $A = \begin{bmatrix} 1 & 0 & 2 \\ 3 & 4 & 5 \\ 2 & 1 & 3 \end{bmatrix}$ dan $B = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 3 & 2 \\ 0 & 2 & 1 \end{bmatrix}$ , berapakah hasil penjumlahan $A + B$ ?

18. Jika $A = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 3 & 2 \\ 0 & 2 & 1 \end{bmatrix}$ , berapakah invers dari matriks $A$ ?

19. Berapakah determinan dari matriks $\begin{bmatrix} -3 & 2 & 1 \\ 0 & 4 & -2 \\ 5 & 1 & 3 \end{bmatrix}$ ?

20. Jika $A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$ dan $B = \begin{bmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{bmatrix}$ , berapakah hasil dari $\text{Tr}(AB^T)$ ?