13 Contoh Soal Persamaan Kuadrat beserta Penyelesaiannya Kelas 11 SMA
Pelajari contoh soal persamaan kuadrat beserta penyelesaiannya untuk jenjang SMA kelas 1. Simak contoh lengkap dengan penyelesaiannya di sini.
Penyelesaiannya:
Soal tersebut merupakan jenis soal persamaan kuadrat dengan cara memfaktorkan sehingga cukup mudah dikerjakan, apalagi persamaannya pendek.
x2+x- 110=0
x-10x+11=0
x-10=0 ∨x+11=0
x-10=0
x=10
x+11=0
x= -11
Biasanya, sebuah soal matematika bisa diselesaikan dengan berbagai cara, termasuk soal di atas. Selain pakai cara pemfaktoran, kamu juga bisa memakai rumus ABC. Penjelasannya, yaitu:
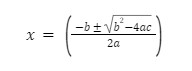
Masih ingat dengan rumus ABC persamaan kuadrat tersebut, kan? Sekarang, kamu tinggal memasukkan angka yang diketahui pada persamaan ke rumus ABC, yakni:
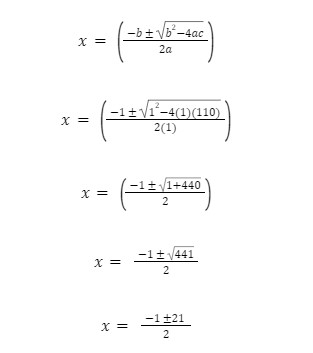
Alhasil, akar-akar yang diperoleh dari rumus ABC yakni:
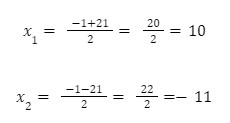
Hasil akar-akarnya sama dengan hasil dari cara sebelumnya yang menggunakan pemfaktoran, kan? Jadi, kamu tinggal memilih cara mana yang dirasa paling mudah atau cepat.
Soal Ketiga
Persamaan kuadrat tentang nilai a, b dan c
Selanjutnya, kamu akan belajar contoh soal persamaan kuadrat beserta penyelesaiannya yang menanyakan tentang nilai a, b dan c.

Advertisement
Diketahui sebuah persamaan kuadrat berbentuk ax2+bx+c=0 mempunyai akar -81 dan 100. Berapakah a, b dan c dari persamaan tersebut?
Penyelesainnya:
Cara paling tepat untuk mengerjakan soal tersebut adalah dengan pemfaktoran. Langkah pertama, cermati dulu dua buah akar tersebut untuk diketahui bentuk aslinya.
x= -81 bisa dijabarkan lebih detail menjadi bentuk faktor yakni x+81=0
x= 100 juga bisa dijabarkan menjadi bentuk faktor yaitu x-100=0
Kemudian, langsung masuk ke pembentukan persamaan kuadratnya:
x+81 x-100=0
x2-100x+81x-8100=0
x2-2x-8100=0
Karena sudah didapat persamaan kuadratnya, maka bisa diketahui nilai yang ditanyakan oleh soal, yaitu:
a sama dengan 1, b sama dengan -2 dan c sama dengan -8100.
Soal Keempat
Berapakah akar-akar yang dimiliki oleh persamaan kuadrat 2×2+8x-4=0?
Penyelesainnya:
Apakah harus menggunakan pemfaktoran? Sebenarnya bisa, tapi lebih baik menggunakan rumus ABC agar lebih cepat.
Berikut pengerjaan soal persamaan kuadrat rumus ABC tersebut:
Dari persamaan kuadrat yang ada, maka bisa diketahui nilai a = 2, b = 8 dan c = -4
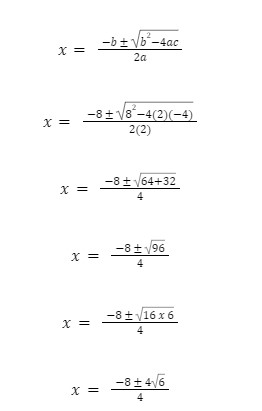
Dengan begitu, akar-akar yang dipunyai oleh persamaan kuadrat tersebut sebagai berikut:
x1= -8+ 464= -4+62
x2= -8- 464= -4-62
Soal Kelima
Berikut ini ada soal lainnya yang sudah Mamikos lampirkan beserta penyelesaiannya untuk kamu cermati. Berikut soalnya:
Akar p dan q dimiliki oleh persamaan kuadrat x2-9x+18=0. Tentukan nilai persamaan
2p2+q2-pq=0 dengan ketentuan p > q!
Penyelesainnya:
Dilihat dari persamaan kuadrat di atas, maka bisa diketahui bahwa cara pemfaktoran akan lebih mudah. Langsung masuk ke penghitungan, ya.
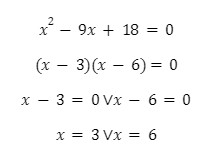
Pada soal, ketentuannya adalah p lebih besar dari q, maka p = 6 dan q = 3 sesuai dengan hasil penghitungan persamaan kuadrat tersebut. Lanjut memasukkan angkanya ke persamaan:
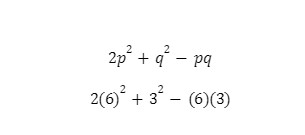
72+9-18=63





