Rangkuman Materi Bentuk Akar, Sifat, Rumus, dan Cara Merasionalkan Lengkap dengan Penjelasannya

Masih kesulitan memahami materi akar? Dapatkan penjelasan secara lebih lengkap di artikel berikut ini.

18 Juli 2024 Fajar Laksana

Sifat Bentuk Akar 2

sifat bentuk akar 2

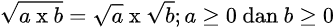
Gambar sifat bentuk akar 2

Sifat Bentuk Akar 3

sifat bentuk akar 3

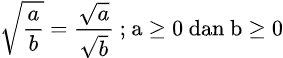
Gambar sifat bentuk akar 3

Rumus – rumus dalam Akar Matematika

Setelah memahami sifat bentuk akar, kini rangkuman materi bentuk akar beranjak ke rumus – rumus dalam akar matematika.

Jadi pada prinsipnya, akar pangkat n dari sebuah bilangan x adalah r, sehingga bisa ditulis dengan kondisi rn = x, lalu dinotasikan menjadi .

Penjelasan untuk keterangan di atas adalah:

n disebut dengan istilah index
x disebut dengan istilah radikan dengan dasar x > 0,
dan, r disebut sebagai resultan atau hasil.

Berikut adalah contohnya yang bisa jadi mudah untuk kamu pahami.

Contoh 1

Contoh 2

Contoh 3

Itulah salah satu rumus dalam rangkuman materi bentuk akar. Rumus di atas tentu saja masih bersifat dasar atau fundamental.

Belum mencapai pada tahap hitungan rumit yang akan memakan waktu pengerjaan lebih lama, namun setidaknya kamu sekarang sudah punya gambaran, bukan?

Baca Juga :

Pengertian Aljabar Kelas 7 SMP beserta Unsur, Rumus, dan Penjelasannya Lengkap

Cara Merasionalkan Akar

Bentuk akar bisa dibilang termasuk menyulitkan, terlebih karena sifatnya yang irasional.

Maka dari itu, bentuk akar yang irasional tersebut perlu untuk dirasionalkan agar dapat lebih mudah untuk diproses hitung.

Sebelum membahas lebih detail tentang cara merasionalkan akar, berikut adalah syarat tertentu yang harus dipenuhi:

1. Pangkat pada faktor bilangan pokok tidak boleh lebih dari indeks akarnya

Contohnya: 

1.

Bentuk sederhana karena pangkat faktor bilangan pokoknya (X) =  1, nilainya kurang dari index akarnya.

2.

Bukan termasuk dalam bentuk sederhana karena pangkat faktor bilangan pokoknya (x) = 5, nilai yang ada lebih besar daripada indeks bagian akarnya.

2. Tidak ada bentuk akar pada bagian penyebut

Contohnya:

1.

Termasuk dalam bentuk sederhana.

2.

Bukan bentuk sederhana karena ada akar pada bagian penyebut.

3. Di dalam akar tidak memuat bilangan pecahan

1.

Termasuk dalam bentuk sederhana.

2.

Bukan termasuk dalam bentuk sederhana karena di dalam akar terdapat pecahan.

Seandainya dalam suatu kasus bentuk tidak sederhana dari sebuah akar tersebut muncul, maka perlu disederhanakan atau dirasionalkan terlebih dahulu.

Untuk cara menyederhanakan atau merasionalkannya bisa dilakukan dengan cara sebagai berikut:

Tags
belajar matematika
bentuk akar
Sifat Akar
Close