Jelaskan yang dimaksud dengan sistem persamaan linear dua variabel Spldv?

SPLDV atau kepanjangan dari sistem persamaan linear dua variabel merupakan dua buah persamaan linier dua variabel yang mempunyai satu penyelesaian yang memenuhi kedua persamaan tersebut. SPLDV ini dapat diselesaikan dengan beberapa metode yang perlu kamu pahami yakni metode grafik, eliminasi, subtitusi, gabungan, determinasi, dan invers matrik.

Apa saja rumus dari Spldv?

Mengenal persamaan linear dua variabel mulai dari metode grafik, substitusi, dan metode lainnya di sini. Secara umum, persamaan linear dua variabel (SPLDV) ditulis dengan bentuk ax + by = c. Untuk keterangannya, x dan y adalah variabel dengan pangkat satu, sedangkan a dan b merupakan koefisien, dan c adalah konstanta.

Apa saja ciri ciri sistem persamaan linear dua variabel?

Kamu mungkin penasaran dengan apa saja yang menjadi ciri-ciri dari sistem persamaan linear dua variabel (SPLDV) tersebut. Di sini kamu akan mengetahui apa saja yang menjadi ciri-ciri dari SPLDV tersebut antara lain (1) Sudah jelas terdiri dari 2 variabel, (2) Kedua variabel pada SPLDV hanya memiliki derajat satu atau berpangkat satu, (3) Menggunakan relasi tanda sama dengan (=), (4) Tidak terdapat perkalian variabel dalam setiap persamaannya.

Penyelesaian Spldv ada 4 cara apa saja sebutkan?

Metode dalam Penyelesaian SPLDV ada empat antara lain adalah Metode eliminasi yang merupakan metode yang dipakai untuk menentukan himpunan penyelesaian dari sistem persamaan linear dua variabel. Caranya dengan menghilangkan (mengeliminasi) salah satu variabel dari sistem persamaan tersebut. Selanjutnya adalah Metode substitusi, Metode gabungan, dan Metode grafik.

Sebutkan fungsi dari Spldv?

Tanpa disadari, sistem persamaan linear dua variabel (SPLDV) ini ternyata memiliki fungsi dan mempunyai manfaat dalam kehidupan sehari-hari. Manfaat dari SPLDV ini antara lain untuk menentukan keuntungan atau laba, mencari harga dasar atau harga pokok suatu barang, hingga membandingkan harga barang.

Rangkuman Materi Sistem Persamaan Linear Dua Variabel (SPLDV) dan Penjelasannya

Perlu kamu tahu bahwa materi pelajaran sistem persamaan linear dua variable cukup kompleks dan membutuhkan konsentrasi jika ingin menguasainya.

15 Agustus 2024 Nana

Beberapa Langkah Menyelesaikan Masalah dengan SPLDV

Sebagaimana yang sudah Mamikos tuliskan, di sini kamu akan menyimak lengkap penjelasan rangkuman materi sistem persamaan linear dua variabel.

Informasi tersebut akan Mamikos lengkapi juga dengan langkah-langkah tertentu untuk menyelesaikan masalah menggunakan SPLDV, antara lain adalah:

Mengganti setiap besaran yang ada dalam masalah tersebut dengan variabel (biasanya akan dilambangkan dengan huruf atau simbol).
Membuat model Matematika dari masalah yang ada. Model Matematika ini akan dirumuskan mengikuti bentuk umum SPLDV (lihat gambar di bab Apa Pengertian Sistem Persamaan Linear Dua Variabel).
Mencari solusi dari model permasalahan tersebut dengan menggunakan metode penyelesaian dari SPLDV.

Macam Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV)

Masih di rangkuman materi sistem persamaan linear dua variabel (SPLDV. Berikutnya Mamikos sudah merangkum apa saja macam-macam penyelesaian yang bisa digunakan untuk menyelesaikan suatu masalah menggunakan sistem persamaan linear dua variabel (SPLDV).

Penjelasan selengkapnya mengenai beberapa macam penyelesaian yang bisa kamu pilih bisa disimak langsung pada uraian sebagai berikut:

1. Metode Grafik

Dalam metode grafik, masalah akan diselesaikan dengan menentukan titik perpotongan dua garis lurus yang merupakan tampilan dari kedua persamaan linear dua variabel.

Di bawah ini Mamikos sertakan juga langkah untuk membantumu menyelesaikan SPLDV dengan metode grafik yang bisa kamu ikuti:

Tentukan titik potong salah satu persamaan linear dengan sumbu X atau dengan sumbu Y.
Hubungkan kedua titik potong dengan menggunakan garis lurus.
Kamu bisa melakukan langkah 1 dan 2 untuk persamaan lain pada SPLDV.
Jika kedua titik berpotongan di (x,y) = (x1, y1), maka penyelesaian SPLD adalah x=x1 dan y=y1.
Apabila kedua titik tidak berpotongan, maka SPLDV tidak memiliki penyelesaian.

Contoh Soal Menggunakan Metode Grafik

Coba lakukan penyelesaian dari sistem persamaan linear dua variabel berikut ini menggunakan metode grafik sebagaimana rumus di atas.

Kamu bisa menyimak contoh soal berikut dengan penyelesaiannya menggunakan metode grafik sebagai berikut:

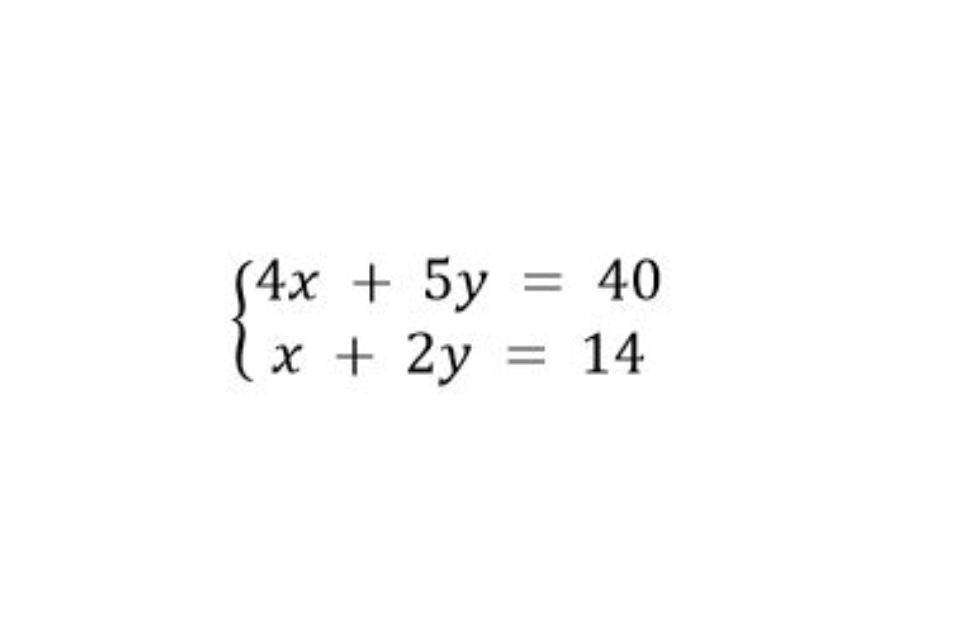
Rangkuman Materi Sistem Persamaan Linear Dua Variable (SPLDV) dan Penjelasannya — detik.com

Penyelesaian soal

Tentukanlah titik perpotongan tiap-tiap persamaan terhadap sumbu X dan Y nya.

Untuk 4x + 5y = 40

Maka, titik perpotongan terhadap sumbu X (y=0) adalah
= 4x + 5(0) = 40
= 4x + 0 = 40
=x = 40/4 = 10
Jadi, garis berpotongan dengan sumbu X di (10,0)

Titik perpotongan terhadap sumbu Y (x=0), penjelasannya

= 4(0) + 5y = 40
= 0 + 5y = 40
=y= 40/5= 8

Rangkuman Materi Sistem Persamaan Linear Dua Variabel (SPLDV) dan Penjelasannya

Beberapa Langkah Menyelesaikan Masalah dengan SPLDV

Macam Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV)

1. Metode Grafik

Contoh Soal Menggunakan Metode Grafik

Penyelesaian soal

Tentang Kami

Job Mamikos

Promosikan Kost Anda

Pusat Bantuan

Blog Mamikos

Singgahsini