7 Macam Bangun Ruang beserta Gambar, Rumus, dan Penjelasannya

Mari belajar mengenali dan mengetahui sifat-sifat bangun ruang Matematika bersama Mamikos!

31 Januari 2024 Lintang Filia

Sifat-sifat Balok

  • Balok memiliki enam sisi, yang terdiri dari dua pasang sisi yang sama panjang dan dua pasang sisi yang lainnya juga sama panjang.
  • Setiap sisi balok berbentuk persegi.
  • Setiap sudut antara dua sisi balok adalah sudut siku-siku (90 derajat).
  • Setiap pasangan sisi yang sejajar memiliki panjang rusuk dan sudut yang sama.
  • Balok memiliki empat diagonal ruang yang menghubungkan dua sudut berlawanan pada balok.
  • Balok memiliki dua diagonal ruang yang menghubungkan dua sudut yang tidak berdekatan pada balok.

Rumus Balok

Rumus Volume Balok

Volume balok dapat dihitung dengan rumus:

V = p * l * t

Keterangan:

p = panjang

l = lebar

t = tinggi balok.

Rumus Luas Permukaan

Luas permukaan balok dapat dihitung dengan rumus:

L = 2pl + 2pt + 2lt

Keterangan:

p = panjang

l = lebar

t = tinggi balok.

Contoh Soal dan Penyelesaiannya

Soal 1

Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 8 cm. Hitunglah volume dari balok tersebut.

Jawaban:

\[ V = 10 \, cm \times 5 \, cm \times 8 \, cm \]

\[ V = 400 \, cm^3 \]

Jadi, volume balok tersebut adalah 400 cm³.

Soal 2

Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 8 cm. Hitunglah luas permukaan dari balok tersebut.

Diketahui:

\[ L = 2 \times (10 \, cm \times 5 \, cm + 10 \, cm \times 8 \, cm + 5 \, cm \times 8 \, cm) \]

\[ L = 2 \times (50 \, cm^2 + 80 \, cm^2 + 40 \, cm^2) \]

\[ L = 2 \times 170 \, cm^2 \]

Baca Juga :

Rumus Bangun Ruang; Luas Permukaan, Volume Dan Contoh Soal

\[ L = 340 \, cm^2 \]

3. Macam-macam Bangun Ruang Prisma

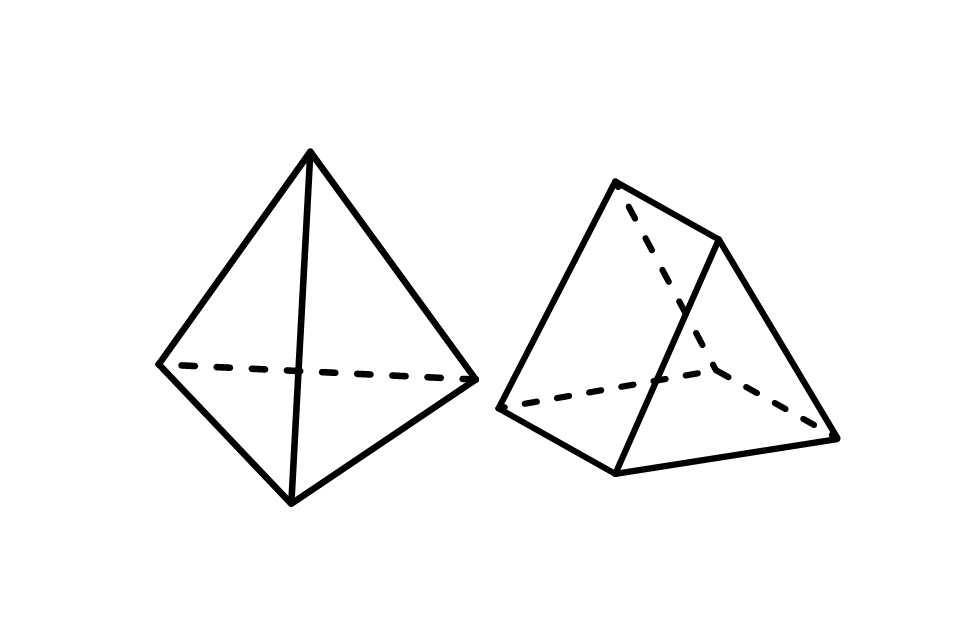
macam macam bangun ruang - prisma
Mamikos

Prisma dapat memiliki berbagai bentuk tergantung pada bentuk alasnya.

Beberapa contoh prisma yang umum dijumpai di antaranya:

  • Prisma Segitiga
  • Prisma Segi Empat
  • Prisma Segi Lima
  • Prisma Segi Enam
  • Prisma Segi-n

Sifat-sifat Prisma

  • Prisma memiliki dua alas yang sejajar dan kedua alas ini berbentuk dan ukurannya sama.
  • Sisi-sisi prisma tegak lurus dengan kedua alasnya. Setiap sisi yang tegak lurus dengan alas berbentuk segi-n.
  • Prisma memiliki diagonal ruang yang menghubungkan dua sudut berlawanan pada salah satu sisi tegaknya.
  • Jumlah rusuk prisma adalah jumlah rusuk kedua alas ditambah dengan jumlah rusuk pada sisi-sisi tegak sesuai dengan bentuk alasnya.

Rumus Prisma

Rumus Volume Prisma

Kamu dapat menghitung volume prisma dengan rumus V = Luas Alas * Tinggi

Di mana Luas Alas adalah luas salah satu alas dan Tinggi adalah jarak antara kedua alas.

Rumus Luas Permukaan

Sedangkan luas permukaan prisma dapat dihitung dengan rumus:

L = 2 * Luas Alas + Keliling Alas * Tinggi

Luas Alas adalah luas salah satu alas, Keliling Alas adalah keliling salah satu alas, dan Tinggi adalah jarak antara kedua alas.

Tags
Bangun Ruang
Materi Matematika
Rumus Bangun Ruang
Close