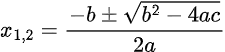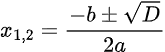Bagaimana cara mencari akar-akar persamaan kuadrat?

Cara mencari akar-akar persamaan kuadrat bisa dengan dimulai berdasarkan rumus yang menghitung besarnya nilai a, b, dan c yang kemudian dibandingkan dengan persamaan dari ax² + bx + c = 0. Lalu, keduanya digantikan menjadi bentuk rumus kuadrat dan tinggal angka hasilnya disederhanakan.

Tuliskan 3 langkah cara mencari akar penyelesaian persamaan kuadrat!

Terdapat sebanyak 3 langkah yang dapat dilakukan untuk mencari akar penyelesaian persamaan kuadrat. Ketiga cara tersebut diantaranya ada menggunakan faktorisasi, kuadrat sempurna, maupun juga rumus kuadratik.

Bagaimana cara menghitung akar kuadrat?

Cara untuk menghitung akar kuadrat bisa dengan mengalikan menggunakan bilangan yang sama. Akar kuadrat menjadi bilangan yang jika dikalikan dengan angka dirinya sendiri, maka nantinya bisa menghasilkan angka yang semula. Cara ini bisa digunakan untuk membantu mencari mana angka yang bisa dikalikan dengan dirinya sendiri. Tujuannya yaitu bisa melihat atau menghasilkan angka sesuai dengan yang diinginkan maupun diperlukan.

Ada 3 cara menyelesaikan persamaan kuadrat apa saja?

Menyelesaikan persamaan kuadrat bisa dengan tiga cara yaitu melalui faktorisasi atau pemfaktoran, kuadrat sempurna, dan rumus kuadrat atau biasa dikenal dengan rumus abc.

Apa saja rumus persamaan kuadrat?

Secara umum, rumus persamaan kuadrat yang digunakan yaitu ax² + bx + c = 0 dengan a ≠ 0.

Belajar Akar-akar Persamaan Kuadrat, Pengertian, Rumus, Jenis, dan Cara Menentukannya

Apakah kamu sedang belajar cara untuk bisa menguasai akar-akar persamaan kuadrat? Simak penjelasan materi akar-akar persamaan kuadrat yang ada di bawah ini.

24 Juli 2024 Fatma

Cara Melakukan Penyelesaian Persamaan Kuadrat

Kali ini terdapat bagian dari materi akar-akar persamaan kuadrat yang akan menjelaskan kepada kamu mengenai cara untuk bisa melakukan penyelesaian atas persamaan kuadrat.

Buat kamu yang sudah mendalami matematika atau sebelumnya membaca terkait dengan persamaan kuadrat, pasti tahu bahwa ada tiga cara yang bisa dilakukan.

Penyelesaian persamaan kuadrat bisa untuk kamu selesaikan dengan cara faktorisasi, melengkapi kuadrat sempurna, maupun juga dengan rumus ABC.

Ketiga cara tersebut menjadi alternatif tersendiri untuk kamu bisa melakukan penyelesaian atas menentukan akar-akar persamaan kuadrat. Berikut ini penjelasan untuk lebih lanjut terkait dengan penyelesaian tersebut.

1. Faktorisasi

Cara pertama yang bisa kamu lakukan untuk menyelesaikan akar-akar persamaan kuadrat yaitu melalui faktorisasi atau memfaktorkan.

Namun, terdapat hal tertentu yang harus kamu pahami dan perhatikan terlebih dahulu sebelum menggunakannya.

Melalui cara ini, terdapat persamaan yang baku dan membuat salah satu ruas yang dimiliki yaitu sebesar nol. Termasuk juga untuk ax² + bx + c = 0 atau 0 = ax² + bx + c.

Kemudian, bentuk dari ax² + bx + c ini sendiri bisa untuk difaktorkan dengan ketentuan sifat yaitu jika pq = 0, maka p = 0 dan q = 0. Hal tersebut membuat penyelesaiannya menjadi seperti berikut.

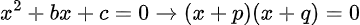
Rumus di atas dengan (p+q) = b dan (p.q) = c.

Kemudian, penyelesaian yang kedua dengan rumus berikut.

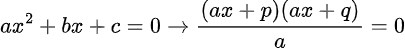
Rumus tersebut dengan ketentuan (p+q) = b dan (p.q) = c.

2. Melengkapi Kuadrat Sempurna

Pada cara yang kedua yaitu bisa dengan menggunakan melengkapi akan kuadrat sempurna.

Saat penyelesaian kuadrat ax² + bx + c dengan cara ini, maka terdapat langkah berikut diantaranya:

Koefisien untuk x² dengan a = 1 atau bisa dibuat jadi 1.
Persamaan ada dalam bentuk x² + mx = n.
Kedua bagian dari ruas persamaan bisa ditambahkan menggunakan (½ koefisien x²).
Persamaan bisa dihadirkan dalam bentuk (x + p)² = q.
Menggunakan persamaan (x + p)² = q ↔ x + p = ± √q.

3. Rumus ABC

Kamu juga bisa menyelesaikan persamaan ini menggunakan rumus ABC.

Namun, persamaan yang digunakan harus bisa dinyatakan dengan bentuk baku dari ax² + bx + c. Kemudian, menentukan nilai yang dimiliki oleh a, b, dan c.

Kamu bisa menggunakan rumus berikut: