Contoh Bentuk Grafik Fungsi Eksponen Kelas 10 SMA beserta Cara Menggambar yang Benar

Salah satu bab dalam materi eksponen berpangkat adalah grafik fungsi eksponen. Seperti apa bentuk dan cara menggambarnya? Dapatkan langkah-langkah mudahnya di artikel ini.

01 Juli 2024 Lintang Filia

5. Range

Range dari fungsi eksponensial tergantung pada apakah fungsi tersebut berbentuk $a \cdot b^x$ atau $a \cdot b^{-x}$ .

Secara umum, untuk $a \cdot b^x$ dengan a > 0 dan b > 0, dengan keterangan sebagai berikut:

Jika b > 1, range adalah semua bilangan real positif (f(x) > 0).
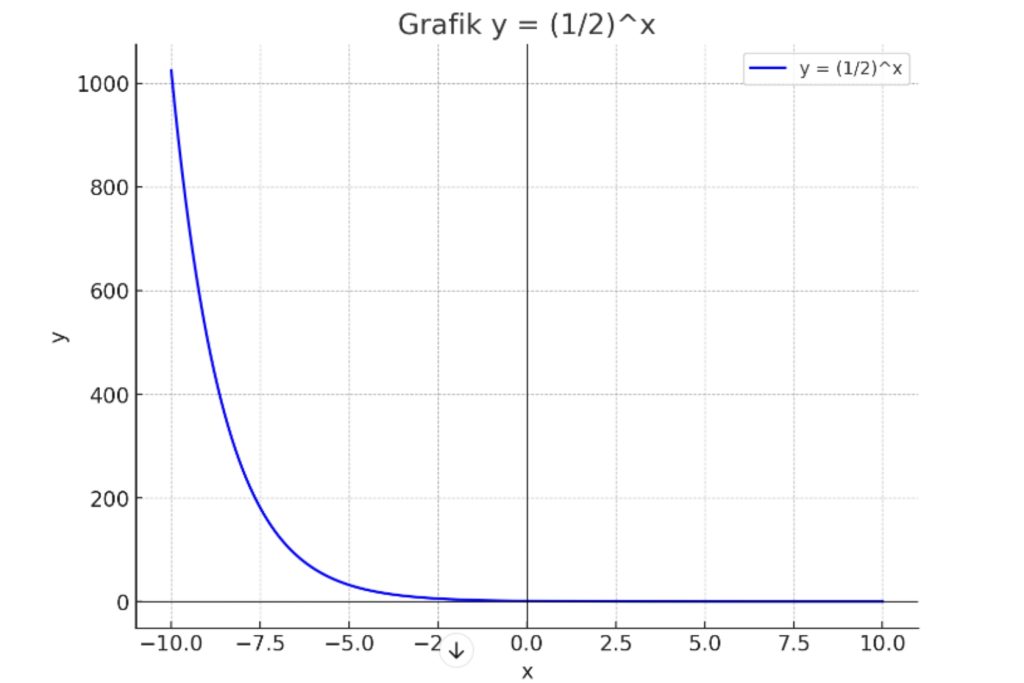
Jika 0 < b < 1, range juga adalah semua bilangan real positif (f(x) > 0).

6. Intersep

Untuk fungsi eksponensial dasar f(x) = b^x, grafiknya memotong sumbu y di titik (0, 1), karena b^0 = 1.

7. Kecekungan

Grafik fungsi eksponensial f(x) = b^x selalu cekung ke atas (konveks).

8. Keberlanjutan

Fungsi eksponensial adalah kontinu untuk semua x \in \mathbb{R}. Tidak ada titik diskontinuitas dalam grafiknya.

9. Diferensiasi dan Integrasi

Turunan: Turunan dari fungsi eksponensial f(x) = e^x adalah f'(x) = e^x.
Integral: Integral dari fungsi eksponensial f(x) = e^x adalah e^x dx = e^x + C, di mana C adalah konstanta integrasi.

Contoh Bentuk Grafik Fungsi Eksponen Kelas 10 SMA

Pada bagian ini Mamikos akan mengajak kamu untuk menggambar contoh bentuk grafik fungsi eksponen yang akan disertai dengan cara yang mudah dan benar.

Nantinya, Mamikos harap kamu bisa mengerjakan contoh soal grafik fungsi eksponen dengan mengikuti langkah-langkah di bawah ini, ya.

1. Fungsi Eksponensial Dasar

Bentuk umumnya adalah y = a^x, di mana a adalah bilangan konstan lebih besar dari 1. Di sini Mamikos akan memberikan contoh bentuk grafik fungsi eksponen kelas 10 SMA, yaitu y = 2^x.

Dari contoh tersebut memiliki ciri-ciri, seperti:

Grafik melewati titik (0, 1).
Grafik meningkat secara eksponensial saat x bertambah.
Grafik mendekati sumbu x (asymptotik ke sumbu x) saat x menuju negatif tak terhingga.

Contoh Grafik Fungsi Eksponen dan Cara Menggambarnya

Pertama yang perlu kamu lakukan adalah menghitung beberapa nilai y untuk berbagai nilai x.

x = -2, y = 2^{-2} = 0.25
x = -1, y = 2^{-1} = 0.5
x = 0, y = 2^0 = 1
x = 1, y = 2^1 = 2

Maka nilai y dan x adalah x = 2, y = 2^2 = 4.

Setelah mendapatkan titik x dan ya, gambarlah titik-titik ini pada koordinat kartesius dengan tepat. Hubungkan titik-titik tersebut dengan sebuah kurva halus yang naik eksponensial saat x bertambah dan mendekati sumbu x saat x menuju negatif tak terhingga.