Materi Bilangan Berpangkat dan Bentuk Akar Kelas 9 SMP, Sifat, Rumus, dan Penjelasannya Lengkap

Tahun ajaran baru segera dimulai. Sebaiknya kamu mulai mempersiapkan diri, termasuk dengan mulai belajar dengan efektif. Oleh karena itu, Mamikos telah membuat rangkuman materi Matematika khusus untuk kamu siswa kelas 9.

02 Juli 2024 Lintang Filia

6. Perkalian Bentuk Akar dengan Pangkat yang Sama

Jika dua bilangan dalam bentuk akar dengan pangkat yang sama dikalikan, hasilnya bisa disederhanakan menjadi satu bentuk akar dengan pangkat yang sama.

Bentuk umum dari perkalian bentuk akar dengan pangkat yang sama adalah \sqrt[n]{a} \times \sqrt[n]{b} = \sqrt[n]{a \times b}.

Contoh: \sqrt[3]{4} \times \sqrt[3]{2} = \sqrt[3]{4 \times 2} = \sqrt[3]{8} = 2.

7. Pembagian Bentuk Akar dengan Pangkat yang Sama

Sifat tersebut terjadi ketika dua bilangan dalam bentuk akar dengan pangkat yang sama dibagi, hasilnya bisa disederhanakan menjadi satu bentuk akar dengan pangkat yang sama.

Rumusnya adalah\sqrt[n]{a} \div \sqrt[n]{b} = \sqrt[n]{\frac{a}{b}}.

Contoh: \sqrt[3]{27} \div \sqrt[3]{3} = \sqrt[3]{\frac{27}{3}} = \sqrt[3]{9} = 2

8. Sifat Distributif Bentuk Akar

Bentuk akar dari hasil kali atau hasil bagi beberapa bilangan dapat dipecah menjadi beberapa bentuk akar.

Rumusnya dengan menggunakan rumus:

\sqrt{a \times b} = \sqrt{a} \times

\sqrt{b}\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}

Contoh:

\sqrt{36 \times 4} = \sqrt{36} \times \sqrt{4} = 6 \times 2 = 12

\sqrt{\frac{81}{9}} = \frac{\sqrt{81}}{\sqrt{9}} = \frac{9}{3} = 3

Baca Juga :

Ringkasan Materi Bahasa Inggris SMP Kelas 9 Semester 1 dan 2 Kurikulum Merdeka

Contoh Soal Materi Bilangan Berpangkat Bentuk Akar

Materi bilangan berpangkat kelas 9 SMP yang terakhir adalah mengerjakan contoh soalnya. Kamu bisa menggunakan sifat-sifat bilangan berpangkat bentuk akar tadi untuk menyelesaikan soal.

Sebagai contoh, Mamikos akan memberikan penyelesaian untuk memecahkan satu soal di bawah ini, ya.

Contoh Soal

Hitung nilai dari 81^{\frac{3}{4}}.

Penyelesaian:

Hal pertama yang harus kamu lakukan adalah ubah soal tersebut ke bentuk akar untuk memudahkan perhitungan: \[81^{\frac{3}{4}} = \sqrt[4]{81^3}\].

Kemudian kita gunakan salah satu sifat bahwa 81 = 3^4 untuk menyederhanakan perhitungan: \[81 = 3^4 \quad \text{jadi} \quad 81^3 = (3^4)^3 = 3^{12}\].

Setelah itu sederhanakan bentuk akarnya dan hitung nilai akhirnya:

\[\sqrt[4]{3^{12}} = 3^{\frac{12}{4}} = 3^3\]

= 33 = 3 x 3 x 3

= 27

Bagaimana? Mudah bukan. Nah, sekarang kamu cobalah untuk mengerjakan beberapa contoh soal bilangan berpangkat di bawah ini dan cocokkan dengan jawabannya, ya. Selamat mencoba!

1. Sederhanakan dan hitung nilai dari \sqrt{49}.

a. 7

b. 6

c. 5

d. 8

Jawaban: a. 7

2. Hitung nilai dari \sqrt[3]{27}.

a. 2

b. 3

c. 4

d. 5

Jawaban: b. 3

3. Berapakah nilai dari \sqrt[4]{16}?

a. 1

b. 4

c. 3

d. 2

Jawaban: d. 2

4. Sederhanakan 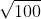\sqrt{100}.

a. 8

b. 9

c. 10

d. 11

Jawaban: c. 10

5. Hitung nilai dari \sqrt[3]{64}.

a. 3

b. 4

c. 5

d. 6

Jawaban: b. 4

6. Jika \sqrt{a} = 6, maka nilai dari \sqrt{4a} adalah …  

a. 6

b. 12

c. 18

d. 24

Jawaban: b. 12

Tags
belajar matematika
kelas 9
Materi Matematika
Close