Materi Trigonometri Kelas 10 SMA Kurikulum Merdeka dan Penjelasannya

Apakah kamu masih belum memahami materi trigonometri yang diajarkan di sekolah? Melalui artikel ini, Mamikos akan mencoba untuk merangkum dan memberikan penjelasan tentang trigonometri,

16 Juli 2024 Lintang Filia

Sudut Segitiga Trigonometri

Materi trigonometri kelas 10 SMA selanjutnya yang akan Mamikos bahas adalah tentang sudut segitiga yang beberapa kali sudah kita sebut. Sebenarnya apa sih yang disebut dengan sudut segitiga trigonometri itu?

Sudut-sudut trigonometri merupakan sudut-sudut yang digunakan dalam operasi hitung trigonometri. Sudut-sudut ini biasanya diukur dalam derajat (°) atau radian (rad).

Berikut adalah beberapa sudut trigonometri yang sering digunakan beserta nilai fungsi trigonometri masing-masing:

1. 0° (0 rad)

sin(0°) = 0
cos(0°) = 1
tan(0°) = 0

2. 30° (π/6 rad)

sin(30°) = 1/2
cos(30°) = √3/2
tan(30°) = √3/3

3. 45° (π/4 rad)

sin(45°) = √2/2
cos(45°) = √2/2
tan(45°) = 1

4. 60° (π/3 rad)

sin(60°) = √3/2
cos(60°) = 1/2
tan(60°) = √3

5. 90° (π/2 rad)

sin(90°) = 1
cos(90°) = 0
tan(90°) = tidak terdefinisi (tidak terhingga)

6. 120° (2π/3 rad)

sin(120°) = √3/2
cos(120°) = -1/2
tan(120°) = -√3

7. 135° (3π/4 rad)

sin(135°) = √2/2
cos(135°) = -√2/2
tan(135°) = -1

8. 150° (5π/6 rad)

sin(150°) = 1/2
cos(150°) = -√3/2
tan(150°) = -√3/3

9. 180° (π rad)

sin(180°) = 0
cos(180°) = -1
tan(180°) = 0

10. 270° (3π/2 rad)

sin(270°) = -1
cos(270°) = 0
tan(270°) = tidak terdefinisi (tidak terhingga)

11. 360° (2π rad)

sin(360°) = 0
cos(360°) = 1
tan(360°) = 0

Berbagai Aturan dalam Trigonometri

Selain fungsi dan sudut segitiga, trigonometri juga memiliki beberapa aturan dan identitas, lho.

Berbagai aturan dalam trigonometri tersebut dipergunakan dalam menghitung dan menyederhanakan perhitungan yang melibatkan panjang sisi dalam dan sudut segitiga.

Berikut adalah penjelasan beberapa aturan dan identitas trigonometri:

1. Aturan Sinus

Aturan sinus menyatakan bahwa perbandingan antara panjang sisi segitiga dengan sinus sudut yang berhadapan adalah konstan untuk semua sisi dan sudut dalam segitiga.

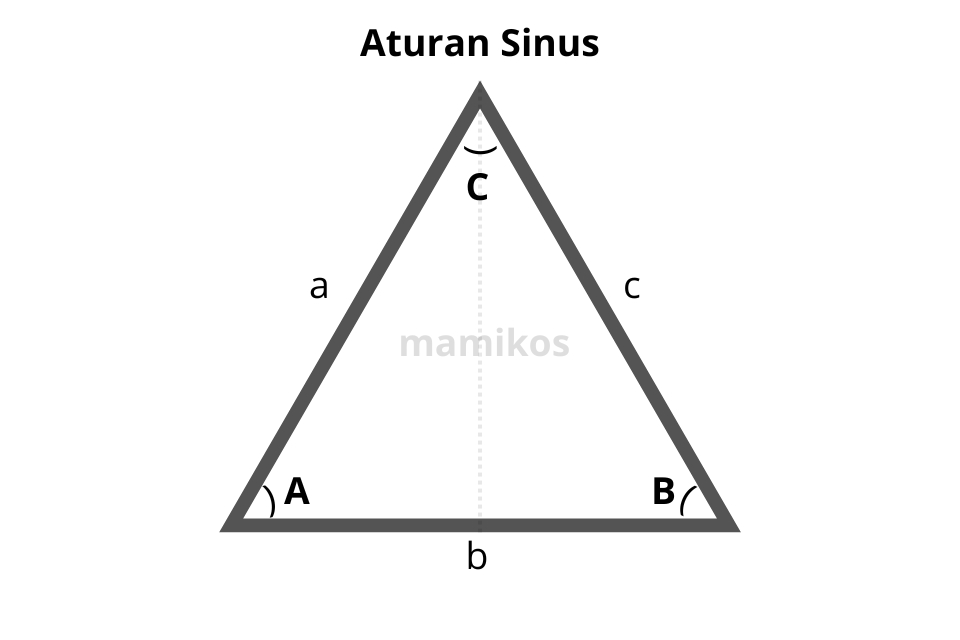
Materi Trigonometri Kelas 10 SMA - Aturan Sinus — Mamikos

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Di mana a, b, dan c adalah panjang sisi-sisi segitiga, dan A, B, dan C adalah sudut-sudut yang berhadapan dengan sisi-sisi tersebut.

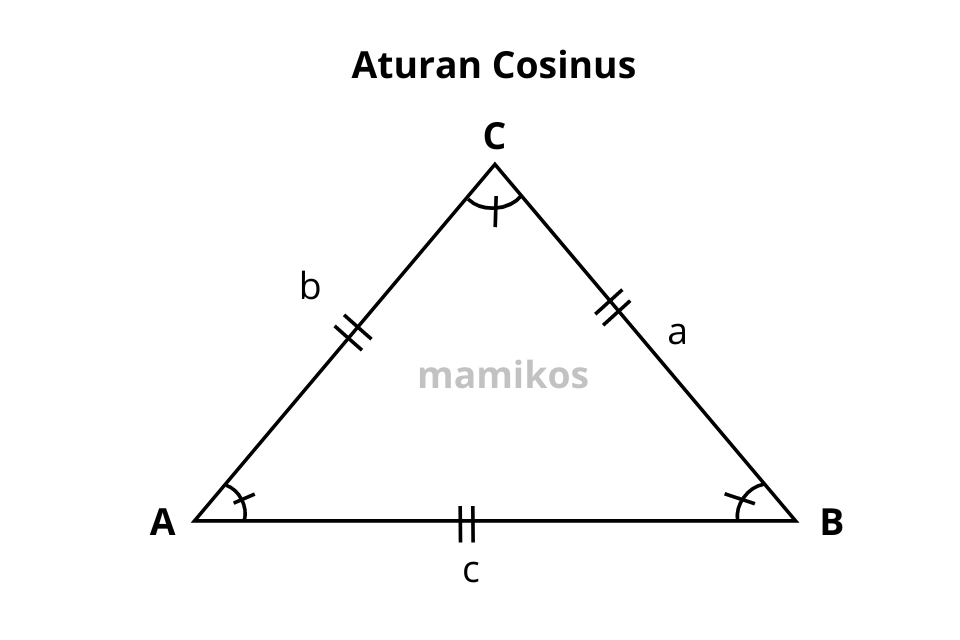
2. Aturan Cosinus

Sedangkan aturan kosinus digunakan untuk menghitung panjang sisi dalam segitiga ketika dua sisi dan sudut yang diapit diketahui. Bisa juga digunakan untuk menghitung sudut ketika tiga sisi diketahui.