Materi Trigonometri Kelas 10 SMA Kurikulum Merdeka dan Penjelasannya

Apakah kamu masih belum memahami materi trigonometri yang diajarkan di sekolah? Melalui artikel ini, Mamikos akan mencoba untuk merangkum dan memberikan penjelasan tentang trigonometri,

16 Juli 2024 Lintang Filia

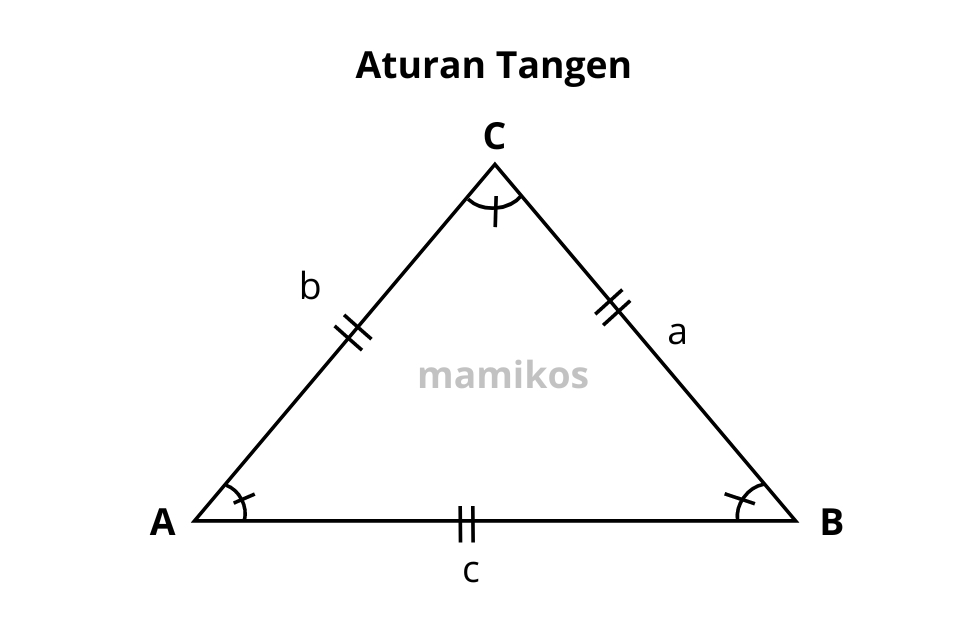
3. Aturan Tangen

Aturan tangen digunakan dalam beberapa kasus tertentu untuk menyelesaikan segitiga, khususnya dalam bentuk yang melibatkan tangen sudut.

Materi Trigonometri Kelas 10 SMA - Aturan Tangen
Mamikos

\[ \frac{a - b}{a + b} = \frac{\tan\left(\frac{A - B}{2}\right)}{\tan\left(\frac{A + B}{2}\right)} \]

Identitas Trigonometri Dasar

Dalam aturan trigonometri terdapat pula identitas dasar yang merupakan hubungan yang selalu benar untuk semua nilai sudut tertentu.

Berikut adalah beberapa identitas dasar trigonometri:

Baca Juga :

Materi Ekonomi Kelas 10 Kurikulum Merdeka Semester 1 dan 2 beserta Penjelasannya

Identitas Pythagoras

\[ \sin^2(\theta) + \cos^2(\theta) = 1 \]

\[ 1 + \tan^2(\theta) = \sec^2(\theta) \]

\[ 1 + \cot^2(\theta) = \csc^2(\theta) \]

Identitas Penjumlahan dan Pengurangan Sudut

\[ \sin(A \pm B) = \sin(A)\cos(B) \pm \cos(A)\sin(B) \]

\[ \cos(A \pm B) = \cos(A)\cos(B) \mp \sin(A)\sin(B) \]

\[ \tan(A \pm B) = \frac{\tan(A) \pm \tan(B)}{1 \mp \tan(A)\tan(B)} \]

Identitas Sudut Ganda

\[ \sin(2\theta) = 2\sin(\theta)\cos(\theta) \]

\[ \cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) \]

\[ \tan(2\theta) = \frac{2\tan(\theta)}{1 - \tan^2(\theta)} \]

Identitas Sudut Setengah

\[ \sin\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{2}} \]

\[ \cos\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 + \cos(\theta)}{2}} \]

\[ \tan\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}} \]

Perbandingan Sudut dan Relasi Trigonometri

Materi trigonometri kelas 10 SMA selanjutnya yang akan kita pelajari adalah tentang perbandingan sudut.

Perbandingan sudut dan sudut relasi dalam trigonometri merupakan konsep-konsep yang penting dalam memahami bagaimana fungsi-fungsi trigonometri bekerja.

Perbandingan Sudut

Perbandingan sudut dalam trigonometri sering kali melibatkan perbandingan antara sudut-sudut yang berbeda pada lingkaran satuan.

Perbandingan sudut tersebut bisa meliputi sudut-sudut dalam kuadran yang berbeda atau sudut-sudut yang memiliki nilai tertentu (seperti 30°, 45°, 60°, 90°, dll.).

Namun sebelum itu, ada beberapa hal yang perlu diperhatikan dalam perbandingan sudut:

1. Sudut Istimewa

Sudut-sudut seperti 30°, 45°, 60°, dan 90° sering kali digunakan dalam perbandingan karena nilai fungsi trigonometri mereka bisa dihitung dengan mudah.

2. Konversi Sudut

Sudut-sudut bisa dikonversi antara derajat dan radian (360° = 2π radian). Misalnya, 180° = π radian, dan seterusnya.

3. Sudut Komplementer dan Suplementer

Sudut Komplementer adalah dua sudut yang jika dijumlahkan menghasilkan 90° (atau π/2 radian). Misalnya, 30° dan 60°.

Sedangkan sudut suplemente terbentuk dari dua sudut yang jika dijumlahkan menghasilkan 180° (atau π radian). Misalnya, 120° dan 60°.

Sudut Relasi dalam Trigonometri

Sudut relasi melibatkan hubungan antara sudut-sudut dan fungsi trigonometri. Beberapa konsep penting dalam sudut relasi yaitu:

1. Sudut Berelasi

Sudut-sudut yang memiliki hubungan tertentu satu sama lain, seperti sudut Kembar yang merupakan sudut yang berbeda 180° atau π radian. Contohnya θ dan θ + 180°.

Kemudian terdapat sudut lawan yang berbeda 360° atau 2π radian. Misalnya, θ dan θ + 360°.

Baca Juga :

Rangkuman Materi Informatika/TIK Kelas 10 Semester 1 dan 2 Kurikulum Merdeka

2. Sudut Berelasi di Kuadran Berbeda

Fungsi trigonometri memiliki tanda yang berbeda tergantung pada kuadran tempat sudut berada, seperti:

  • Kuadran I (0° – 90°): Semua fungsi trigonometri positif.
  • Kuadran II (90° – 180°): Sinus positif, cosinus dan tangen negatif.
  • Kuadran III (180° – 270°): Tangen positif, sinus dan cosinus negatif.
  • Kuadran IV (270° – 360°): Cosinus positif, sinus dan tangen negatif.
Tags
Materi Matematika
Rumus Trigonometri
Trigonometri
Close