Cara Merasionalkan Bentuk Akar dengan Mudah beserta Contoh Soal Kelas 9

Bentuk akar perlu dirasionalkan agar bisa menyederhanakan operasi aljabar dengan lebih mudah.

29 Oktober 2023 Uyo Yahya

Contoh soal 4

Tentukanlah hasil dari operasi bentuk akar yang ada di bawah ini:

\frac{8}{3 + \sqrt{5}} = ...

A. 6 - 2\sqrt{5}

B. 6+2\sqrt{5}

C. 12 - 2\sqrt{5}

D. 12 + 2\sqrt{5}

Penyelesaian:

Untuk menyelesaikan operasi aljabar bentuk akar di atas, kamu bisa melakukannya dengan cara berikut ini:

\frac{8}{3+\sqrt{5}}=\frac{8}{3+\sqrt{5}} . 1

=\frac{8}{3 +\sqrt{5}} . \frac{3 - \sqrt{5}}{3 - \sqrt{5}}

=\frac{8\left ( 3-\sqrt{5} \right )}{\left ( 3+\sqrt{5} \right )-\left ( 3-\sqrt{5} \right )}

=\frac{8\left ( 3 - \sqrt{5} \right )}{\left ( 9-5 \right )}

= \frac{8\left ( 3-\sqrt{5} \right )}{4}

=\frac{2 \left ( 3-\sqrt{5} \right )}{1}

= 6 -2\sqrt{5}

Jadi, jawaban yang benar untuk operasi rasional bentuk akar dari contoh di atas adalah A. 6 - 2\sqrt{5} 

Baca Juga :

Penting untuk Diketahui, Ini Materi Persamaan dan Pertidaksamaan Nilai Mutlak!

Contoh soal 5

Tentukanlah hasil dari operasi bentuk akar yang ada di bawah ini:

2\sqrt{27} . \sqrt{32} : \sqrt{48} = ...

A. 4\sqrt{3}

B. 5\sqrt{2}

C. 3\sqrt{3}

D. 6\sqrt{2}

Penyelesaian:

Untuk menyelesaikan operasi aljabar bentuk akar di atas, kamu bisa melakukannya dengan cara berikut ini:

2\sqrt{27} . \sqrt{32} : \sqrt{48} = ...

= 2\sqrt{9.3}. \sqrt{16.2} :\sqrt{16.3}

= 2 . 3\sqrt{3} . 4\sqrt{2}: 4\sqrt{3}

=\frac{6\sqrt{3}.4\sqrt{2}}{4\sqrt{3}}

=6\sqrt{2}

Jadi, jawaban yang benar untuk operasi merasionalkan bentuk akar di atas adalah D. 6\sqrt{2}

Baca Juga :

Cara Mengubah Persen ke Desimal dan Sebaliknya beserta Contoh Soal

Cara Merasionalkan Bentuk Akar pada Bilangan Pecahan

Bentuk akar juga hadir dalam bilangan pecahan. Oleh karena itu, saat mendapati soal pecahan dengan bentuk akar di dalamnya maka kamu perlu tahu juga cara merasionalkan bentuk akar pada bilangan pecahan.

Perlu diketahui bahwa dalam merasionalkan bentuk akar pecahan, yang perlu dirasionalkan adalah penyebutnya saja.

Tujuan dari merasionalkan penyebut pecahan ini adalah sebagai salah satu cara dalam mencari bentuk sederhana pada sebuah operasi aljabar.

Selain itu, juga bertujuan agar penulisan atau perhitungan aljabar bermuatan bentuk akar menjadi lebih mudah.

Perlu menjadi catatan juga bahwa merasionalkan penyebut dari pecahan bentuk akar sama sekali tidak akan merubah nilai dari aljabarnya sendiri.

Baca Juga :

Inilah Penjelasan Lengkap Konsep Persamaan dan Pertidaksamaan Nilai Mutlak Linear Satu Variabel Hingga Karakteristiknya

Dalam cara merasionalkan bentuk akar pecahan, dikenal sebuah istilah yang disebut dengan akar konjugat atau akar sekawan. 

Bentuk \left ( \sqrt{a}-\sqrt{b} \right ) bentuk konjugatnya adalah \left ( \sqrt{a} + \sqrt{b}\right ) dan begitu juga sebaliknya.

  • \left ( a+\sqrt{b} \right )\left ( a-\sqrt{b} \right )=a^{2}-b
  • \left ( \sqrt{a}+b \right )\left ( \sqrt{a}-b \right )= a-b^{2}
  • \left ( \sqrt{a}+\sqrt{b} \right )\left ( \sqrt{a}-\sqrt{b} \right )= a-b

Selain akar konjugat, cara menyederhanakan bentuk aljabar bentuk akar adalah dengan menarik akar kuadrat.

Cara Merasionalkan Penyebut Pecahan Bentuk 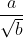\frac{a}{\sqrt{b}}

Cara untuk merasionalkan penyebut pada bentuk akar bilangan becahan \frac{a}{\sqrt{b}} adalah dengan operasi seperti di bawah ini:

\frac{a}{\sqrt{b}}=\frac{a}{\sqrt{b}}. 1

=\frac{a}{\sqrt{b}} . \frac{\sqrt{b}}{\sqrt{b}}

=\frac{a\sqrt{b}}{b}

=\frac{a}{b}\sqrt{b}

Cara Merasionalkan Penyebut Pecahan Bentuk \frac{a}{\sqrt{b}+\sqrt{c}}

Cara merasionalkan penyebut pecahan yang memiliki bentuk akar dengan bentuk \frac{a}{\sqrt{b}+\sqrt{c}} adalah dengan operasi seperti di bawah ini:

\frac{a}{\sqrt{b}+\sqrt{b}} = \frac{a}{\sqrt{b}+\sqrt{b}} . 1

=\frac{a}{\sqrt{b}+\sqrt{c}}. \frac{\sqrt{b}-\sqrt{c}}{\sqrt{b}-\sqrt{c}}

=\frac{a\left ( \sqrt{b}-\sqrt{c} \right )}{b-c}

=\frac{a}{b-c}\left ( \sqrt{b} - \sqrt{c}\right )

Tags
bentuk akar
cara merasionalkan bentuk akar
Matematika
Close